Improving Python performance for numerical routines
By Ryan Pepper
When writing numerical software in Python, there is a somewhat overwhelming array of options for tackling performance issues. From experience, it’s very hard to actually evaluate which of these options is “best” for performance without actually trying them in a specific scenario, and to understand what is happening requires an understanding of both the Python, NumPy, and lower level language’s call stack, the input arguments of the particular routine, and the system on which the code is designed to run on. In this blog post I’ll walk through a few different strategies to improve a performance critical routine and compare the perforamnce and the advantages and disadvantages.
NumPy
Let’s consider a pretty basic method for a simple mathematical calculation $\sqrt{\frac{x^2}{12}}$ as a normal developer might write it, and let’s assume that this has been found via profiling to be the “hot path” in the code, which is where the bulk of time is spent:
import numpy as np
def mathematical_routine_numpy(x: np.ndarray[np.float64], output: np.ndarray[np.float64]) -> None:
output[:] = np.sqrt(input*input/12)
I’ve used NumPy here by default rather than using Python lists and for loops. The main benefit to performance of using NumPy over pure Python is that NumPy arrays are contiguous in memory (all elements are stored consecutively), and it utilises methods written in compiled languages which use single-instruction multiple-data (SIMD) in order perform operations. Modern CPUs of all architectures (x86-64, ARM, etc.) have additional instruction sets that allow vector operations, so for e.g. when multiplying two arrays together, depending on exactly the datatype, the instruction sets your CPU has (e.g. AVX2, AVX512 on Intel, SVE on ARM), and what target architecture NumPy was compiled against, it might take 2, 4 or 8 values at a time to operate on.
Improving the NumPy routine
Looking at the initial implementation of the code, it looks OK, but a number of temporary NumPy arrays are allocated at each stage of the calculation (for e.g. when input*input is computed). If the input arrays are large, this can add a significant time cost to the performance of the code just through the cost of memory allocation, and significatly increase the peak memory usage. We can therefore do a small refactor, using the output array as intermediate storage and doing calculations in-place:
def mathematical_routine_numpy_faster(x: np.ndarray[np.float64], output: np.ndarray[np.float64]) -> None:
output[:] = input
outout[:] *= input
output[:] /= 12
np.sqrt(output, out=output)
As an alternative, to this, we can also look at Numba. Numba effectively takes an annotated Python function, generates LLVM bytecode from the routine and just-in-time compiles it using the LLVM compiler to gain C or Fortran like performance. There are a number of ways of using Numba, but in general a good rule of thumb is that to get the best performance, you need to run it using the ’nopython’ mode to really take advantage of it. An implementation of our routine using Numba looks like:
@numba.njit(["void(float64[:], float64[:])"], parallel=True)
def mathematical_routine_numba(input, output):
for i in numba.prange(input.shape[0]):
output[i] = np.sqrt(input[i]*input[i]/12)
Here, njit rather than the standard jit routine you might see in Numba tutorials enforces that the routine must not use arbitrary Python routines but a restricted subset, the annotations specify that the input arguments are two 64-bit floating point 1-D arrays, and the parallel=True argument tells the compiler to use OpenMP to provide paralellism over the loop. The first time that a Numba function is called, LLVM bytecode is generated and then compiled, and this can add a performance overhead if for e.g. the function is not frequently used. Notably, getting the best performance out of Numba requires us to do our operations element-wise - this allows us to avoid multiple traverses over the input and output arrays.
C + Cython
In addition to the Numba version, we can very simply write the equivalent C function, also making use of OpenMP:
// functions.h
#pragma once
void mathematical_routine(double *input, double* output, int N);
// functions.c
#include <math.h>
void mathematical_routine(double* input, double* output, int N) {
#pragma omp parallel for
for (int i = 0; i < N; i++) {
output[i] = sqrt(input[i]*input[i]/12);
}
}
Making this available within Python can be done in a number of different ways (SWIG, ctypes, Pybind11, hand writing an extension module using the Python C API) but my personal preference is to use Cython for a decent balance between control and simplicity. Cython is a language in it’s own right, and you can write functions that get compiled to C in a similar way to Numba, but here we’re just using this functionality to wrap our C function:
# cfunctions.pyx
import cython
# The function definition from the header file is effectively copied and pasted into the
# Cython code here.
cdef extern from "functions.h":
void mathematical_routine(double* input, double* output, int N)
def mathematical_routine_c(double[:] input, double[:] output):
"""
Wrapper function that passes the input arguments and extra information like their length to
the C function.
"""
assert len(input) == len(output)
N = len(input)
mathematical_routine(&input[0], &output[0], N)
This file needs to be run through the Cython transpiler, which takes the cfunctions.pyx file and outputs cfunctions.c which can in turn be compiled using the compiler of your choice. There are a number of ways to configure the build process, but probably the best way is to set up a proper library with a pyproject.toml file:
# pyproject.toml
[build-system]
requires = ["setuptools", "cython"]
build-backend = "setuptools.build_meta"
[project]
name = "mathematical_routines" # as it would appear on PyPI
version = "0.0.1"
and then add the compilation(s) as a stage in the wheel build process by adding Extension modules via the setuptools library.
# setup.py
from setuptools import Extension, setup
# Enable optimizations, build to support the specific microarchitecture, and enable OpenMP for parallelism
extra_compile_args = ["-O2", "-march=native", "-fopenmp"]
extra_link_args = ["-fopenmp"]
setup(
ext_modules=[
Extension(
name="mathematical_routines.cfunctions",
sources=["mathematical_routines/functions.c", "mathematical_routines/cfunctions.pyx"],
extra_compile_args=extra_compile_args,
extra_link_args=extra_link_args,
),
]
)
~
Note that here, we’ve included the C file defining the functions as another source file, though if you are using an external C library, it is better to use it’s own build system, and just link against it as necessary; this is often preferable even for when the only use case of the C files is for use as Python extensions. From here, we can run a build of the code while developing like:
# To build the extension, and place them in the same place in the source directory as the source files:
python setup.py build_ext --inplace
Our routine can then be imported in Python just by doing:
from mathematical_routines.cfunctions import mathematical_routine_c
Benchmarking
You can see below the benchmarks testing the function for 10^N elements, run fairly unscientifically on my pretty ancient 2-core 2013 Macbook. The code used to generate these results is available here
| $10^N$ | Numpy | Numpy (Optimised) | Numba | Cython + C |
|---|---|---|---|---|
| 4 | 0.007539 | 0.00552827 | 0.00631435 | 0.0099843 |
| 5 | 0.0822677 | 0.0668484 | 0.0622144 | 0.0680254 |
| 6 | 0.992097 | 0.705271 | 0.531437 | 0.533711 |
| 7 | 9.51496 | 6.7119 | 5.18282 | 5.33702 |
| 8 | 170.29 | 99.1852 | 53.5006 | 53.9295 |
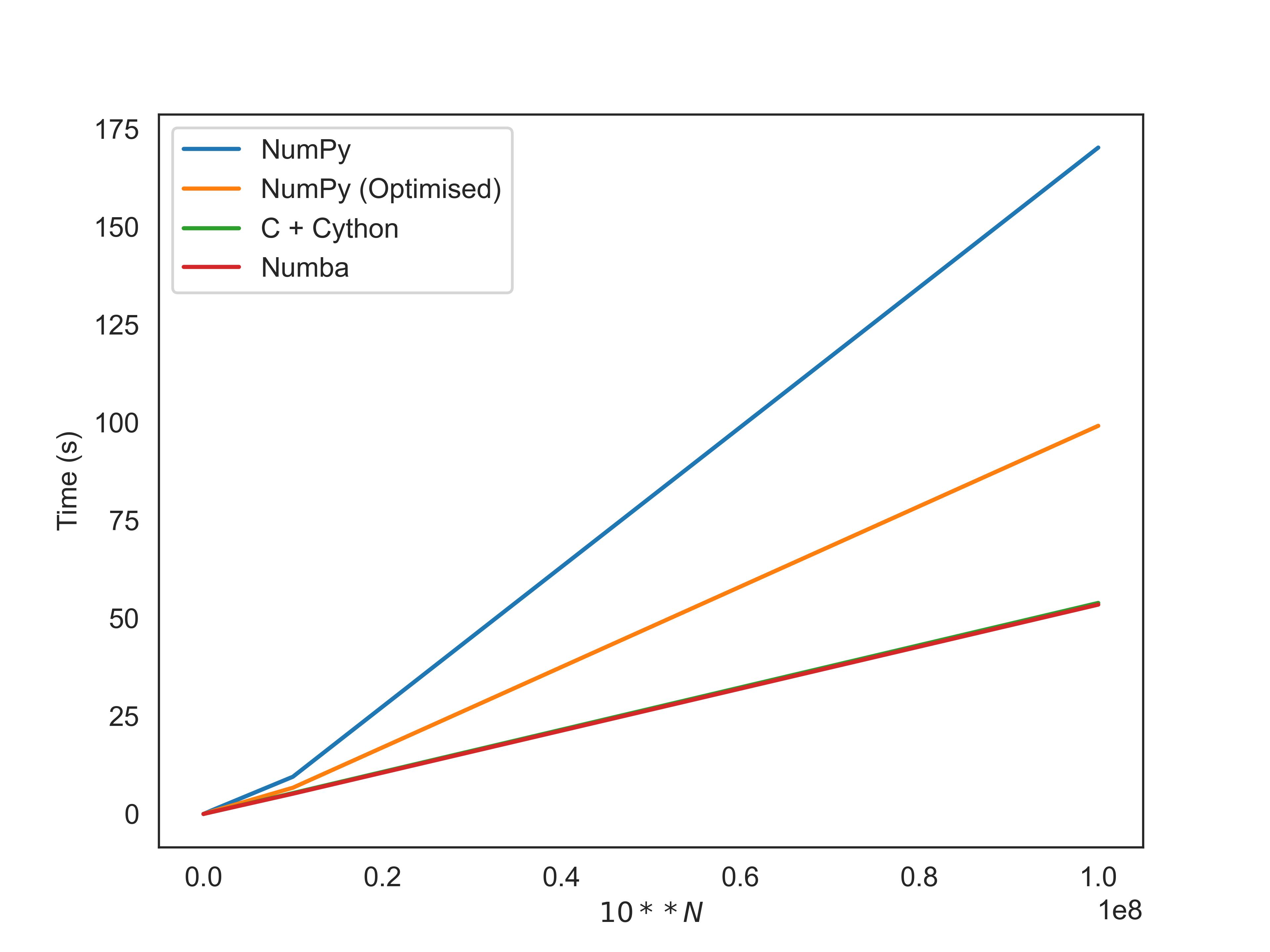
Note that here, the JIT compilation stage was not counted in the metrics for Numba. It’s a clear draw between Numba and Cython, with our optimised Numpy still significantly better than the naively written code. In terms of simplicity, there’s something to be said for pure NumPy, though it’s clear that to get the best out of it, you have to be very careful and understand exactly what might happen for a given operation, which we showed by re-architecting the method to prevent temporary arrays from being allocated. We get a significant additional performance benefit from using Numba and C even though the code is much the same, because we traverse over the input array exactly once rather than repeatedly, and the compiler will take care of SIMD optimisations for us through autovectorization.
Between Numba and C, it’s clear that Numba has a simplicity in tooling and they are broadly equivalent in terms of performance. Distributing a Python library that uses Numba is no different to any other Python library, though it’s worth considering that LLVM which is needed for the JIT compilation is a fairly significant runtime dependency and also can’t be used on some of the more obscure processor architectures. It is now possible to ahead of time compile for Numba accelerated routines, which reduces the ’time to start’ when using them, and removes the need for LLVM at runtime, much as a C extension doesn’t require a compiler at runtime. Where Numba does fall down compared to using C/etc. is when you want to make use of external C libraries that already exist - while it is possible to expose and use them through Numba, I’ve found that it’s considerably simpler to do this in Cython or Pybind11. Both options are feasible for releasing code that has been somewhat obfuscated through compilation, which is useful in the commercial world.